捌拾壹- 量子态层析 以及 布洛赫球 (2)

4. 那多比特呢！？

紧接上一段 捌拾- 量子态层析 以及 布洛赫球 (1)

理论上来说，三个量子比特的密度函数，出来的是一个 2 的三次方

( 别问我为什么知道，我也不知道物理意义 )

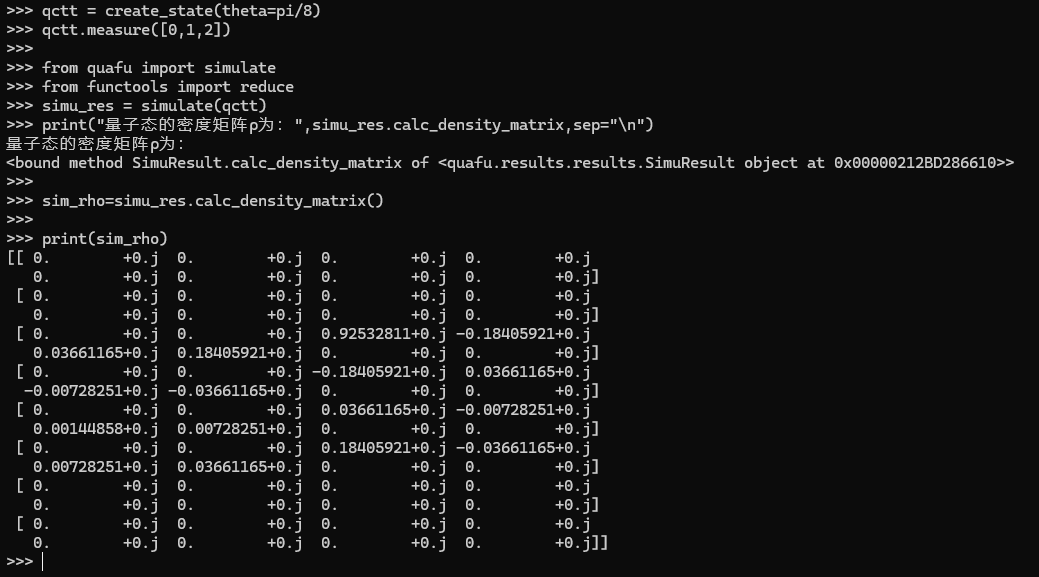
alt text

但，在 0.4.6 里面怎么计算期望值呢？

于是求助伟大的 AI ， 找出方法是：

alt text

oh！那简单了！

写出简单 Python 函数


from quafu import QuantumCircuit, simulate, Task
import numpy as np
import matplotlib.pyplot as plt
from numpy import pi, cos, sin, sqrt

def create_state(theta):
    qc = QuantumCircuit(3)
    qc.ry(0, theta)
    qc.x(1)
    qc.cnot(0,2)
    qc.ry(2, -theta)
    qc.cnot(0,1)
    # qc.barrier([0,1])
    return qc

qctt = create_state(theta=pi/8)
qctt.measure([0,1,2])

from quafu import simulate
from functools import reduce
simu_res = simulate(qctt)
print("量子态的密度矩阵ρ为：",simu_res.calc_density_matrix,sep="\n")

sim_rho=simu_res.calc_density_matrix()
# 定义 Pauli Z 矩阵
sigma_Z = np.array([[1, 0], [0, -1]])
# 定义单位矩阵
sigma_I = np.array([[1, 0], [0, 1]])

sub_obsexp=[]

sub_obsexp.append(np.trace(np.dot(sim_rho,reduce(np.kron, [sigma_Z,sigma_I,sigma_I]))).real)
sub_obsexp.append(np.trace(np.dot(sim_rho,reduce(np.kron, [sigma_I,sigma_Z,sigma_I]))).real)
sub_obsexp.append(np.trace(np.dot(sim_rho,reduce(np.kron, [sigma_I,sigma_I,sigma_Z]))).real)
sub_obsexp.append(np.trace(np.dot(sim_rho,reduce(np.kron, [sigma_Z,sigma_Z,sigma_I]))).real)
sub_obsexp.append(np.trace(np.dot(sim_rho,reduce(np.kron, [sigma_Z,sigma_Z,sigma_Z]))).real)
sub_obsexp.append(np.trace(np.dot(sim_rho,reduce(np.kron, [sigma_I,sigma_Z,sigma_Z]))).real)
print(sub_obsexp)

其中我觉得这段里面最牛逼的就是那个 Numpy 的矩阵运算

先用 np.kron 求张量积，再把密度函数跟这个扩张了的观测算符进行 点乘 ，然后求 迹

Oh，完美！

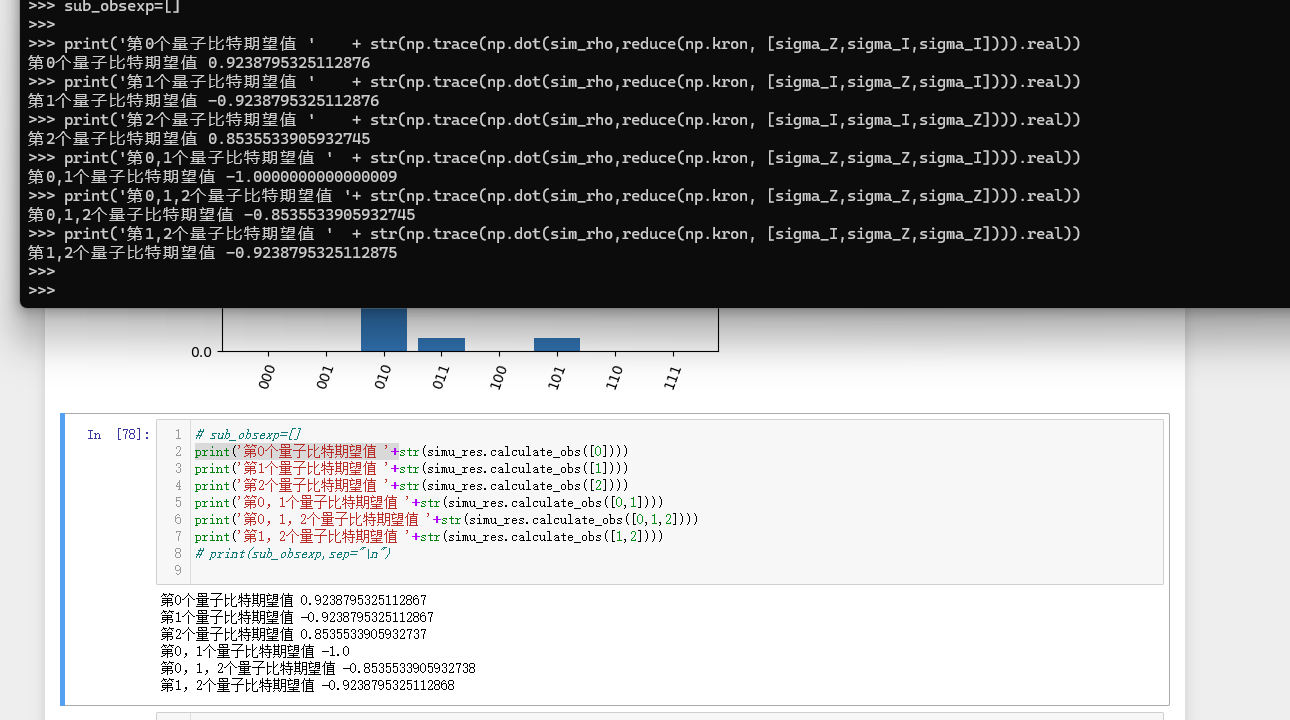
alt text

5. 量子态是否混态

这个可以通过对整体密度矩阵的布洛赫矢量来看看每个量子比特是否混态

按我理解，如果单个比特，或多比特但无纠缠的量子比特，其基本是纯态的，而有纠缠或与其他量子比特有关联的就是混态 ( 我总觉得这个想法不太符合物理描述，但…就意思意思 )

可以通过下述代码，模拟 0/1 量子比特是有关联，而 2 量子比特是在一起观测，但无关联的



# 2. 三个量子比特中，其中一个量子比特的 量子态 是否纯态
from quafu import QuantumCircuit, simulate, Task
import numpy as np
import matplotlib.pyplot as plt
from numpy import pi, cos, sin, sqrt

def create_state(theta):
    qc = QuantumCircuit(3)
    qc.ry(0, theta)
    qc.x(1)
    # qc.cnot(0,2)
    # qc.ry(2, -theta)
    qc.cnot(0,1)
    # qc.barrier([0,1])
    return qc

qctt = create_state(theta=pi/8)
qctt.measure([0,1,2])

from quafu import simulate
from functools import reduce
simu_res = simulate(qctt)
print("量子态的密度矩阵ρ为：",simu_res.calc_density_matrix,sep="\n")

sim_rho=simu_res.calc_density_matrix()
# 定义 Pauli Z 矩阵
sigma_Z = np.array([[1, 0], [0, -1]])
# 定义单位矩阵
sigma_I = np.array([[1, 0], [0, 1]])
# 定义泡利X矩阵
sigma_X = np.array([[0, 1],[1, 0]])
# 定义泡利Y矩阵
sigma_Y = np.array([[0, -1j],[1j, 0]])

sub_obsexp=[]

q0ZExpV=np.trace(np.dot(sim_rho,reduce(np.kron, [sigma_Z,sigma_I,sigma_I]))).real
q0YExpV=np.trace(np.dot(sim_rho,reduce(np.kron, [sigma_Y,sigma_I,sigma_I]))).real
q0XExpV=np.trace(np.dot(sim_rho,reduce(np.kron, [sigma_X,sigma_I,sigma_I]))).real

q1ZExpV=np.trace(np.dot(sim_rho,reduce(np.kron, [sigma_I,sigma_Z,sigma_I]))).real
q1YExpV=np.trace(np.dot(sim_rho,reduce(np.kron, [sigma_I,sigma_Y,sigma_I]))).real
q1XExpV=np.trace(np.dot(sim_rho,reduce(np.kron, [sigma_I,sigma_X,sigma_I]))).real

q2ZExpV=np.trace(np.dot(sim_rho,reduce(np.kron, [sigma_I,sigma_I,sigma_Z]))).real
q2YExpV=np.trace(np.dot(sim_rho,reduce(np.kron, [sigma_I,sigma_I,sigma_Y]))).real
q2XExpV=np.trace(np.dot(sim_rho,reduce(np.kron, [sigma_I,sigma_I,sigma_X]))).real


print('第0个布洛赫矢量长度 ' + str(q0ZExpV*q0ZExpV+q0YExpV*q0YExpV+q0XExpV*q0XExpV))
print('第1个布洛赫矢量长度 ' + str(q1ZExpV*q1ZExpV+q1YExpV*q1YExpV+q1XExpV*q1XExpV))
print('第2个布洛赫矢量长度 ' + str(q2ZExpV*q2ZExpV+q2YExpV*q2YExpV+q2XExpV*q2XExpV))

结果如

alt text

6. 但实机测量的是什么呢？

不知道为何，以前实机的任务十几秒就返回了，现在的任务却要一天了…

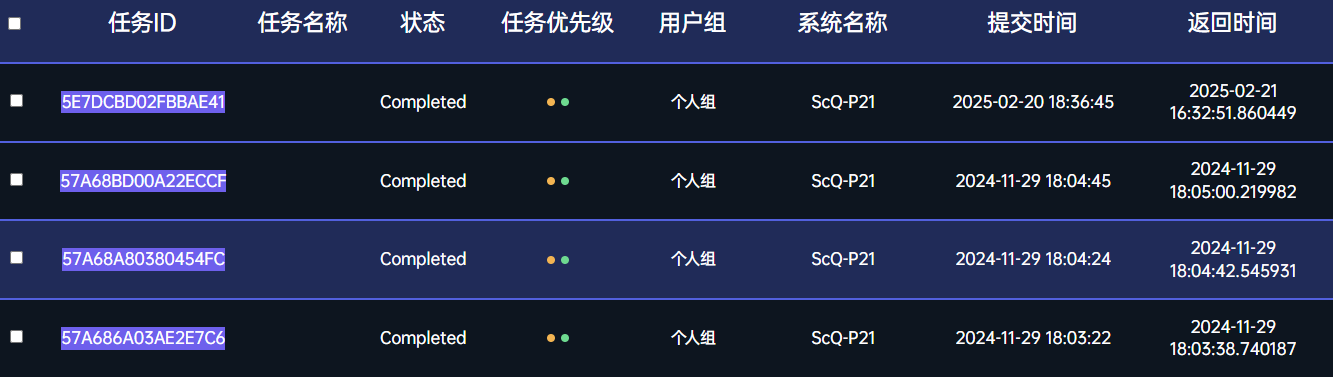
alt text

可怜

好，咱们来看看实机测量得到的是什么

咱们先到官网注册

量子计算云平台

然后回得到 Token

可以看教程测试试一下实机怎么 send 量子电路上去运行的，但因为现在太慢了，于是我选择用以前的上传的任务来看看

alt text

居然没有模拟测试时返回最全信息的密度函数！！！只有各种测量结果的概率！！？！？

查找了一堆之后，看到说，真正 量子计算 时，只会对每个量子比特进行 一次测量 ( 就是 Z 轴的状态 ) ，所以我们把多次测量的 结果 ( 每个粒子在 Z 轴是 0 或 1 的状态 ) 组合就看出这个量子电路跑完后，各结果的 概率 。

7. 那模拟能算出来为啥还要实机？

模拟得出来的结果更全 ( 有密度矩阵 ) ，为何我们还用实机的只有各比特 Z 轴测量结果的方法呢？

哈..我也问过 AI ，他们说，模拟结果运算量其实很大，在多量子比特运算时，整个量子电路的算子矩阵就会超级大 ( 而且是指数级的 ) ，所以量子比特多到某个程度，电脑就很难模拟了

感觉，我得继续去努力了，拿着上面的实验结果，继续去看回贝尔不等式的教程呗

Twitter Icon
Facebook Icon