捌拾贰- 贝尔不等式 (2)
1. 贝尔不等式理解
我感觉我前期理解的不是很对 柒拾玖- 贝尔不等式 …
思来想去几天,感觉贝尔不等式应该是这样来的
因为观测的值只有可能是 ±1 (别问我为什么) , 设观测角度 Q 值为 +1 的概率为 a , -1 的概率为 b , Q 的数学期望值为
E(Q) = a * 1 + b * (-1) = a - b
设观测角度 S 值为 +1 的概率为 c , -1 的概率为 d , S 的数学期望值为
E(S) = c * 1 + d * (-1) = c - d
而观测 Q 跟 S 为同一个值的概率为
E(QS) = + ac + bd - ad - bc
E(QS) = a ( c - d) - b ( c - d )
E(QS) = ( a - b ) * ( c - d ) = E(Q) * E(S)
然后就像教程上展示的
其实之前一直不理解, 明明量子计算中, 电路测量出来是两个量子比特方向 相等的概率, 而不是两个值相乘
虽然数学上来说两者是一样的, 但主要还是对 QS + RS + RT − QT = ( Q + R ) S + ( R − Q ) T 的物理意义有点不解 ( 例如如果测量结果是 0 跟 1 的话, 那么上述就不成立了 )
通过上述过程就好理解很多了.. ( 虽然还是对物理意义有点含糊 )
2. 那到底破坏了什么呢?
到底量子计算破坏了贝尔不等式的什么呢?
还是不懂…
但遇到了一些更难懂的东西
3. E(Q) ≠ E(Q) ?
在第 1 点的描述中, 我们可以理解 E(Q) 跟 E(S) 其实是独立的 ( 或根据初始状态确定的 )
且根据 局域性 , 无论 E(S) 测出什么, 其实并不会影响 E(Q)
但神奇的东西来了,我们来研究研究
假设我们设置这样一个电路, 分别有 q0 和 q1 两个量子比特, 其中只关注 q0
我们要做的就是把 q0 旋转一个角度 θ , 并且观测它在这个角度的值, 让 q1 保持在某个角度, 并让 q0 和 q1 两个量子比特不做任何纠缠
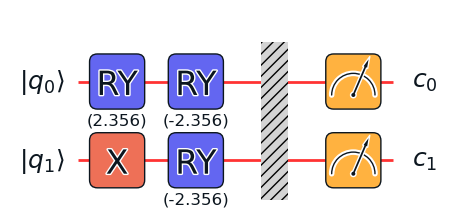
就像这样测 (红色是 q0 跟 q1 的测量角度, 绿色是 q0 旋转后的角度, 紫色是 q1 的旋转角度 固定在 pi 上):
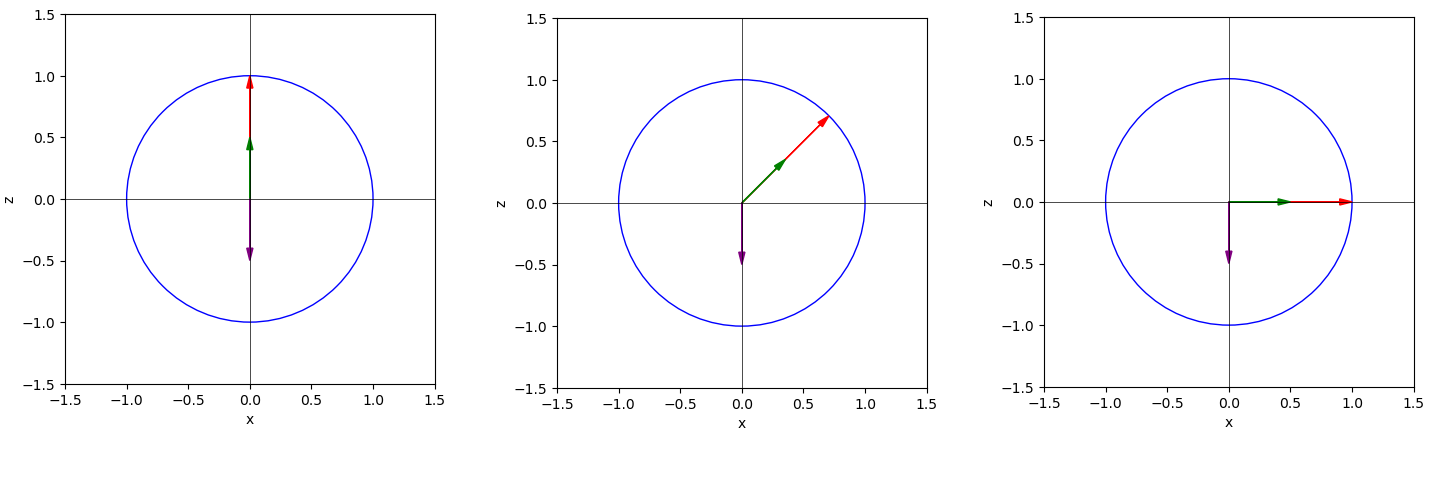
可以预想, 并且 无论对初始偏角怎么旋转 , 实际测出来, 这个 q0 永远测出来是 +1
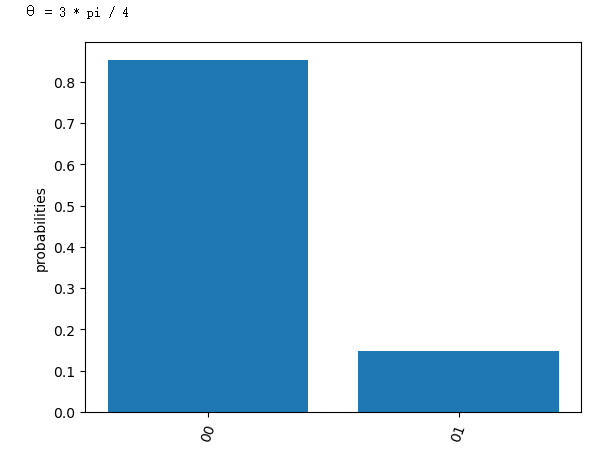
但当我把它跟另一个量子比特进行关联, 例如用一个 CNOT 门 ( 当 q0 是 |
0> 的时候, q1 不反转, 从原来的 | 0> 变成 | 1>, 但相反的话, 则 q1 反转 ) 把他们关联起来 |
这时候, 我们看到一个很独特的现象, 例如我们还是测量以下这个, 只不过在测量前我们用了 CNOT 门, 其中 q0 是 控制量子比特, q1 是 目标量子比特
还是测量上面那几个角度, 但!!!神奇的一幕出现了..
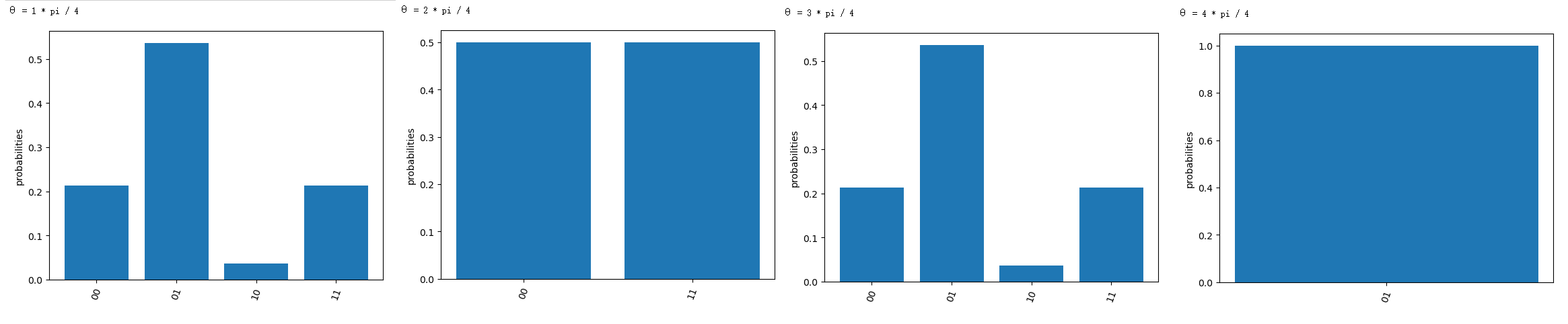
| 为什么量子比特 q0 会出现不等于 | 0> 的情况呢!!!!!!!!!!!! |
1) 第一步
我们先看简单的 θ = 0 * pi / 2 的情况 ( 我们想步进 pi / 2 的情况来看, 而为什么不是步进 pi / 4 呢? 因为太复杂..我数学比较差 )
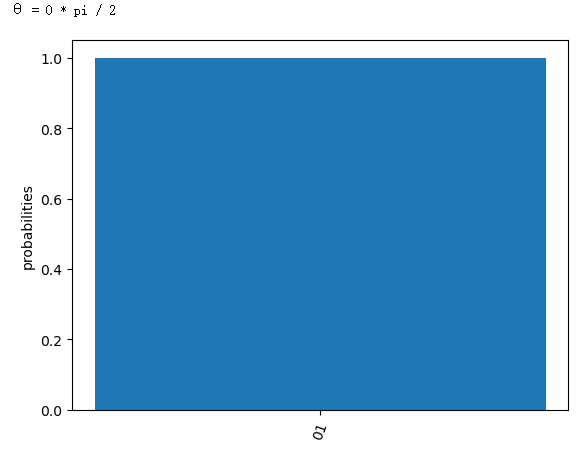
| 这个好理解, 因为 q0 不动, 再原地测量, 肯定是 | 0> , 而 q1 旋转了 pi , 所以是 | 1> 没错 |
然后!
2) 第二步!!
θ = 1 * pi / 2
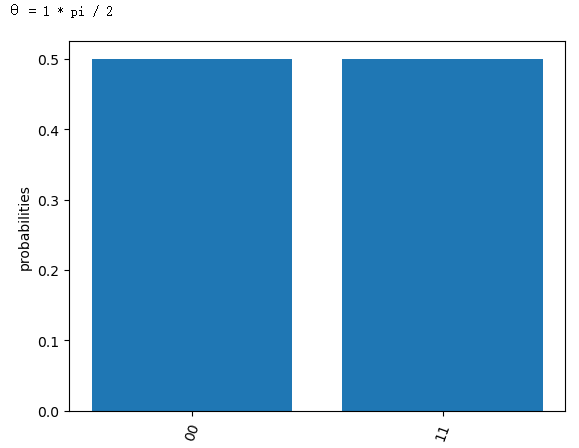
为什么!?为什么它会有 00 和 11 !?
好了, 经典的理解在这里已经崩塌了..
通过结果, 逻辑反向推理证明:
-
明显 q1 的结果影响了 q0 , 因为当 q0 初次旋转时就不是 0> , 而通过 CNOT 门 会影响 q1 的结果 -
但如果要影响 q1 , q0 必须要有一个确定的状态 0> 或 1>
这个结果证明了两件事情:
-
q0 的测量结果影响了 q1 , 而不是初始的时候确定状态确定最后结果 ( 不然两者就会像没有纠缠一样, q0 恒等于 0> ) - 如果这两个量子比特互相以光速互相背离飞行, 但结果又是互相影响的, 因为第1点, 证明了超光速作用是存在的
4. 后续
这里面还真有太多的概念是上网查的..这里没列明, 例如:
-
ψ> 跟 <ψ 的矩阵表示 - 例如各种门的矩阵形式
- 例如矩阵的运算, 例如 迹 等
后续得写一个东西好好补充一下各种内容并专门开个贴记录
之前大学时学量子力学还没学过 狄拉克符号 .. 而且就学到 一维无限深势阱 这些..唉….
真羡慕大学生能好好的有时间学习..为啥成年人的生活那么苦困