捌拾捌- 海森堡不确定性原理 (2)

5. 书接上一回

上次看到 ΔA⋅ΔB ，具体是怎样推导的呢？也理解了

\[\Delta A=( \langle A^2 \rangle - \langle A \rangle^2 ) ^{1/2} \\\]

但不知道为什么，我总觉得上述公式是没啥用

回看 上节 的第4点，得出

6. 找到一个简单的推导过程

alt text

alt text

从数学看来很简单，但有两个疑问

  1. 对易子 跟 反对易子 是什么逻辑，怎样推导的？
  2. 为什么只保留 对易子？

6.1) “对易子” 和 “反对易子”

先从概念上说：

alt text

给一个物理定义上的例子：

alt text

alt text

再用基础的 泡利算符 作为例子：

alt text

alt text

大模型给我们延伸了一个内容：

alt text

这里就绝望了….什么叫 李代数 、什么叫 克利福德代数（Clifford algebra） 、又什么叫 狄拉克方程与费米子场

一头雾水，但大概能看清

6.2) 为什么 “只保留对易子”？

alt text

alt text

可以理解为，其实关注的重点不是 AB + BA

而是调换顺序后的差 AB - BA

alt text

就是先测量哪一个，再测量另外一个值时，在经典物理是没差别的，但在 量子物理 语境下，就是有差别的了

7. 泡利算符的例子 - 回到教程本身

我们看回教程本身 的 1.3 点

计算得知

alt text

故教程中的公式为：

更具体地，设量子态

\[|\psi \rangle=cos \frac{\theta}{2}|0 \rangle + e^{i\phi}sin\frac{\theta}{2}|1 \rangle\]

其中 𝜙 和 𝜃 为对量子比特的转动

\[\langle \psi |X| \psi \rangle = sin \theta cos \phi\] \[\langle \psi |Y| \psi \rangle = sin \theta sin \phi\] \[\langle \psi |Z| \psi \rangle = cos \theta\] \[\langle \psi |X^2| \psi \rangle = \langle \psi |Y^2| \psi \rangle = 1\]

上述为算符的期望值，X、Y、Z 分别为三种不同 泡利算符

且因为

\[\Delta X \Delta Y \geq \ |\langle Z \rangle |\] \[\Delta X=( \langle X^2 \rangle - \langle X \rangle^2 ) ^{1/2} \\\]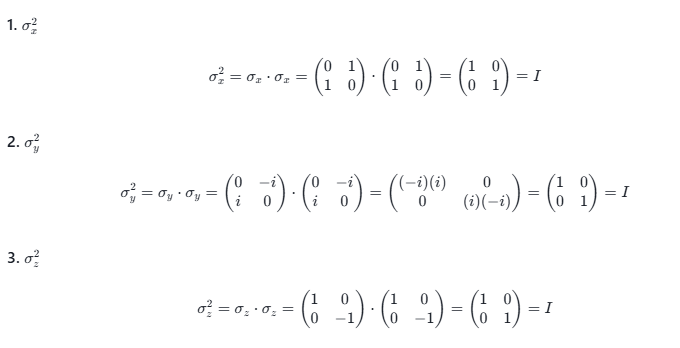

alt text

所以

\[\begin{aligned} \left[\Delta (X) \Delta (Y)\right]^2-| \langle Z \rangle|^2&=(1-{sin}^2 \theta {cos}^2 \phi)(1- {sin}^2 \theta {sin}^2 \phi)-{cos}^2 \theta \\ &={cos}^2 \phi {sin}^2 \phi {sin}^4 \theta \geq 0 \end{aligned}\]

8. PyQuafu 的例子代码

因为真机排队排得很慢，于是我只用模拟的结果

# 引用包
import numpy as np
import matplotlib.pyplot as plt
from quafu import QuantumCircuit, simulate, Task
from numpy import pi, cos, sin

# 构建量子
def construct_circuit(theta):
    qc = QuantumCircuit(3)
    for i in range(3):  # 创建一个3量子比特的电路, 量子态: |0> --> |ψ> = cos(θ/2)|0> + exp(i*pi/4)*sin(θ/2)|1>
        qc.ry(i, theta)
        qc.rz(i, pi/4)
    qc.barrier([0,1,2])
    qc.ry(0, -pi/2)   # 转化测量基为X的本征态
    qc.rx(1, pi/2)    # 转化测量基为Y的本征态
    qc.measure([0,1,2])
    return qc

# 以 θ = 𝜋/2 作为例子绘制电路
q = construct_circuit(pi/2)
q.plot_circuit()

下面的代码我是删除了某些真机的配置 ( 而且都是过期的，后端名字都不是那些了 )

# 模拟的内容
def uncertainty_principle_demo(theta_num = 20):
    # θ 的步长多长
    theta_step = pi/theta_num
    theta = []  # 保存θ的值
    obsexp = []  # 保存 EX,EY,EZ
    for i in range(theta_num):
        theta_i = i*theta_step
        # 配置当前的 θ 值
        qc = construct_circuit(theta = theta_i)
        sub_obsexp=[] # 保存此次循环中 EX,EY,EZ 的值
        # 丢进去做模拟！！！！！！
        simu_res = simulate(qc)
        for i in range(3):
            sub_obsexp.append(simu_res.calculate_obs([i]))
        # 插入实验的 θ 以及 期望值
        theta.append(theta_i)
        obsexp.append(sub_obsexp)
    return theta,obsexp

# 根据上面第 7 点的公式，手算的值
def theoretical_value(theta, phi = pi/4):
    return (sin(phi)**2)*(cos(phi)**2)*(sin(theta)**4)  # [Δ(X)Δ(Y)]^2-|<Z>|^2
x = np.linspace(0, pi, 100)
y = theoretical_value(x)

好了，准备都准备好了，我们开始画图！

# 画模拟结果为蓝色一点点的函数
def plot_theoretical_value(x,y):
    plt.plot(x, y, label="Theoretical value: sin(φ)^2*cos(φ)^2*sin(θ)^4")
    plt.xlabel("theta")
    plt.ylabel("(Δ(X)Δ(Y))^2-|<Z>|^2")
    plt.legend(loc="upper center", bbox_to_anchor=(0.5, 1.15))

# 模拟结果
theta, obsexp = uncertainty_principle_demo(theta_num = 20)
# 根据反馈的期望值计算结果
res=[(1-obsexp[i][0]**2)*(1-obsexp[i][1]**2)-obsexp[i][2]**2 for i in range(len(obsexp))]  # [Δ(X)Δ(Y)]^2-|<Z>|^2
for i in range(len(res)):
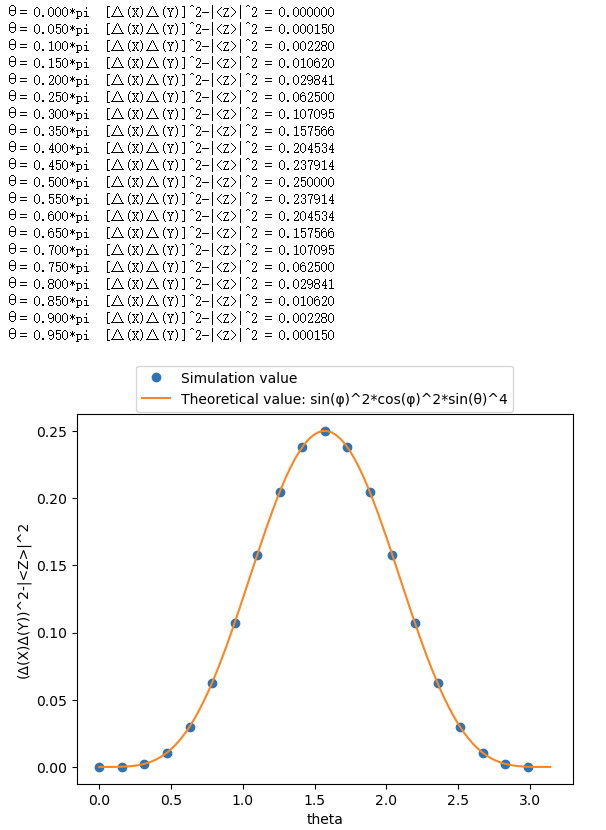
    print("θ= {:.3f}*pi ".format(theta[i]/pi),"[Δ(X)Δ(Y)]^2-|<Z>|^2 = {:.6f}".format(res[i]))  # 展示结果数据
# 展示结果图
plt.plot(theta, res, "o",label="Simulation value")
plot_theoretical_value(x,y)
plt.show()

输出的结果如下：

alt text

9. 这些东西好废脑子

之前请教过某些数学博士，他说看这些公式其实还挺好懂，但为什么我看着一脸懵…

看来我还得好好学习

俺先去努力工作先

Twitter Icon
Facebook Icon