量子计算 - 02 - 数学基础与狄拉克符号
以下数据均从各大地方搜刮下来,有些是 AI 生成的…很难一一列明出处
AI 生成的有 ChatGLM ( 智谱清言 ) , OpenAI 等
1. 量子比特的基本状态

2. 计算数学期望值

3. 矩阵相乘

4. 矩阵的迹

5. 张量积

6. 共轭转置
计算 ∣ψ⟩ 的共轭转置 ⟨ψ∣ 是由:


7. 幺正性 (Unitarity)

快速观测一个算子是否符合 幺正性

8. 矩阵的行列式 (Determinant)

9. 量子态的概率


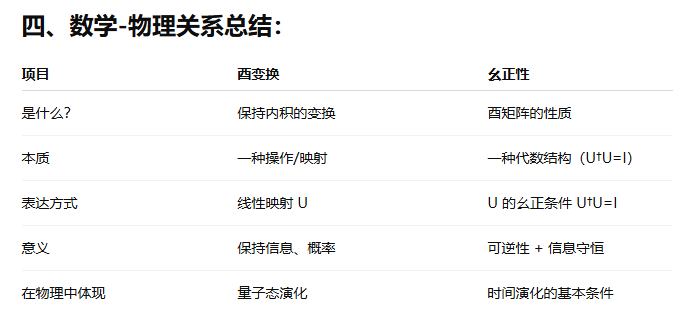
10. 酉变换 (Unitary Transformation)

“幺正矩阵”(Unitary Matrix)和“酉矩阵”(Unitary Matrix)指的是完全相同的概念。
11. 傅里叶变换
一般可理解为时频变换,得知一个时变函数,把他转换为相应的频率对应函数

12. 伴随 - 厄密共轭
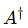
(读作“A dagger” 或 “A 的伴随”)就是算符 A 的厄米共轭(Hermitian conjugate 或 adjoint 操作)



12. 厄米算子 ( Hermitian operator )

13. 期望值的线性性质


14. 范数 ( Norm )

15. 柯西-施瓦茨不等式 ( Cauchy-Schwarz Inequality )


相对来说,就是两个向量 ( 设为 A 和 B ),其中这个不等式就是说两个向量的点积,小于两个向量长度的乘积
如公式 u · v = |u| |v| cos(θ)
16. 点积 ( Dot Product ) 、内积 ( Inner Product ) 、标量积 ( Scalar Product )

17. 量子电路的狄拉克描述形式
在量子理论中,顺序是极其重要的。原因在于:
17.1) 张量积不是交换的:
\[A \otimes B \neq B \otimes A\]这两个操作作用在系统
\[\left|{\psi}\right\rangle = \left|{a}\right\rangle \otimes \left|{b}\right\rangle\]上时结果截然不同。例如:
\[(H \otimes I)\left|{01}\right\rangle \neq (I \otimes H)\left|{01}\right\rangle\]前者将 H 作用在第一个比特,后者作用在第二个。
张量积空间中的对象是有序对,也就是说:
\[\left|{a}\right\rangle \otimes \left|{b}\right\rangle \neq \left|{b}\right\rangle \otimes \left|{a}\right\rangle\]除非你明确使用 SWAP 门 做交换。
17.2) 酉变换链也是非交换的:
\[U_3 U_2 U_1 \left|{\psi}\right\rangle \neq U_1 U_2 U_3 \left|{\psi}\right\rangle\]在数学上,这是因为一般而言:
\[[U_i, U_j] \neq 0 \quad (\text{即 } U_i U_j \neq U_j U_i)\]这和经典线性代数中的矩阵乘法一样,顺序会改变最终的变换效果。
17.3) 酉变换的顺序对应于时间演化顺序
狄拉克形式:
\[\left|{\psi_{\text{out}}}\right\rangle = U_n \cdots U_2 U_1 \left|{\psi_{\text{in}}}\right\rangle\]这个表达式中,每个
\[U\_k\]是一个酉算符,也可以理解为量子电路中的一个“门”,作用在某个时间步。
\[U\_1\]最先作用在初态上;
\[U\_2\]再作用于
\[U\_1\left|{\psi}\right\rangle\];最后
\[U\_n\]完成最后的操作。
这就像时间的箭头从左向右,虽然我们在公式中是从右向左乘算符,但这正是它的时间演化之秩序。
量子演化是有方向的!不是热力学第二定律意义上的时间箭头,而是逻辑上因果演算的顺序结构。
17.4) 实验上顺序的重要性
考虑以下两个电路:
- 电路 A:先 Hadamard 后 CNOT(即产生 Bell 态)
- 电路 B:先 CNOT 后 Hadamard(同样门,但顺序不同)
它们产生的量子态完全不同。
电路 A:先 Hadamard 再 CNOT
- 作用 \(H \otimes I\):
- 再作用 CNOT:
电路 B:先 CNOT 再 Hadamard
- 首先作用 CNOT:
- 然后作用 \(H \otimes I\):
结论:它们不一样!但初态为 |00> 时,B 电路恰好与 A 的第一步相同。
- 电路 A 得到的是 Bell 态:
- 电路 B 仅施加了 Hadamard 到第一个比特,结果仍是未纠缠态
您说这两个结果一样,是因为我在前文举的电路 B 的推导只走了一步,它在 CNOT 后立即施加 \(H \otimes I\),其实产生的只是:
\[(H \otimes I)U_{\text{CNOT}} \left|{00}\right\rangle = (H \otimes I)\left|{00}\right\rangle = \frac{1}{\sqrt{2}}(\left|{00}\right\rangle + \left|{10}\right\rangle)\]这 与 Bell 态不同,因为
\[\frac{1}{\sqrt{2}}(\left|{00}\right\rangle + \left|{10}\right\rangle)\]是可分的(不纠缠),而
\[\frac{1}{\sqrt{2}}(\left|{00}\right\rangle + \left|{11}\right\rangle)\]是纠缠态。
关键点:纠缠性的差异揭示了量子门顺序的重要性
虽然在某些特定初态下(如
\[\left|{00}\right\rangle\]),部分门序列看似“结果一致”,但这只是偶然的对易性发生了。
但若我们考虑更一般的输入,比如
\[\left|{10}\right\rangle\]或
\[\left|{+0}\right\rangle\],那么两种顺序将给出完全不同的结果和测量统计。
数学补充:一般而言,
\[U_{\text{CNOT}} (H \otimes I) \neq (H \otimes I) U_{\text{CNOT}}\]这两者之差源于非交换性,所以门顺序一变,通常:
- 态的纠缠度变了
- 测量结果概率变了
- 整个干涉结构也变了
18. 复共轭
18.1) 复共轭表达
其中 * 表示复共轭。对于一个复数 z = a + bi,它的复共轭
定义为 a - bi 。在这个表达式中, z 和 z* 分别表示某个复数的实部和虚部的组合以及其实部相同、虚部相反的组合。具体来说,表达式中的
意味着 z 减去它的复共轭等于 z 虚部的两倍乘以虚数单位 i 。这是因为
会消去实部,只留下虚部的两倍。
在矩阵代数中,对于一个给定的矩阵 z,其复共轭矩阵 z* (也称为共轭转置或 Hermitian 转置)是通过将矩阵中的每个元素取其复共轭,然后对矩阵进行转置得到的。
对于一个 3x3 的矩阵 z,假设其元素为 \(z_{ij}\),其中 i 和 j 分别是行和列的索引(从 1 到 3),那么 z 的复共轭矩阵 z* 的元素将是 \(\overline{z_{ji}} ,其中 \overline{z_{ji}} 表示 z_{ji} 的复共轭。\)
例如,如果矩阵 z 是:
那么 z 的复共轭矩阵 z* 将是:
其中,
\[\overline{a + bi}\]表示 a - bi,即复数 a + bi 的复共轭。同理,其他元素也取其复共轭。然后,矩阵 z* 是通过将 z 的行和列互换得到的,即 z* 是 z 的转置。
18.2) 厄米算子的复共轭
\[\left( \langle \psi | \hat{O} | \psi \rangle \right)^* = \langle \psi | \hat{O}^\dagger | \psi \rangle\]所以我们计算:
\[\left( \langle \psi | XY | \psi \rangle \right)^* = \langle \psi | (XY)^\dagger | \psi \rangle\]运用共轭反转法则:
\[(XY)^\dagger = Y^\dagger X^\dagger = YX \quad \text{(因为 X,Y 是厄米的)}\]于是有:
\[\left( \langle XY \rangle \right)^* = \langle YX \rangle\]